An introductory logic course, designed for students from a broad range of disciplines, from mathematics and computer science to drama and creative writing. It is also designed to reflect aspects of the logical tradition (going back to Aristotle) as well as the practical applicability (for example for the construction of Boolean circuits). Below one finds a detailed description of the course with many of its special features.
Logic & Proofs
$0 – $80
- Description
- Additional information
- Active engagement
- The LogicLab
- Individual Learner
- Academic Use
- Detailed Content
- Versions and Features
- How to Access Logic & Proofs
- Open & Free features
Description
Logic is a remarkable discipline. It is deeply rooted in the past going back to its first systematic presentation in Aristotle’s work. In its modern form, it has not only expanded Aristotelian Logic in dramatic ways, but it has also become foundational, e.g., for linguistics, computer science, cognitive science, and artificial intelligence. It is, of course, deeply intertwined with philosophy and mathematics as correctness of argumentation is particularly crucial for these abstract disciplines.
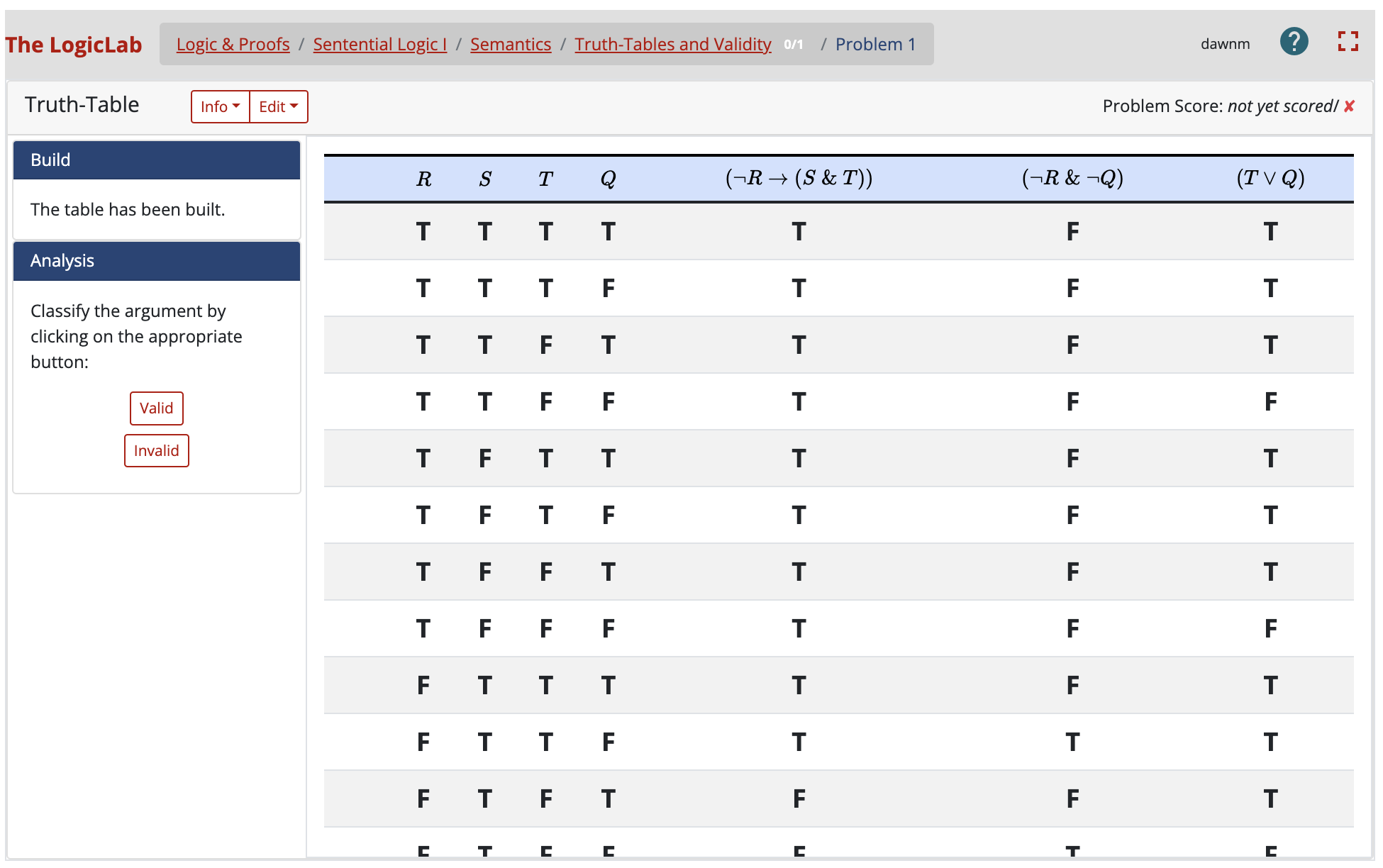
Logic & Proofs is a rigorous introduction to modern symbolic logic that covers both sentential and predicate logic (including identity). The crucial skills of recognizing the (in-)correctness of arguments are honed by working in the LogicLab: in derivation or proof problems, students learn to construct complex arguments in a strategically guided way; in truth table and truth-tree problems, the emphasis is on systematically finding counterexamples.
The LogicLab is a central part in bringing these core topics to vivid life. Indeed, the course has been constructed to provide support for individual learning through active engagement. That is a most important feature and applies across all versions of Logic & Proofs, whether the course is taken by an individual learner or a student at an academic institution.
The active engagement is furthermore strengthened by using the Standalone LogicLab to formulate and explore new logical problems.
Additional information
| Versions: | CURIOUS EXPLORER'S COURSE (Open and Free version), INDEPENDENT LEARNER'S COURSE (self-paced with certificate of completion; no teacher), INSTRUCTOR'S ACADEMIC COURSE (for use with your students) |
|---|
Active engagement
Logic & Proofs is designed for students from a broad range of disciplines, from mathematics and computer science to drama and creative writing. It is also designed for someone who would like to get a real insight into modern symbolic logic. The course is highly interactive and engaging; it brings a fresh perspective to classical material. These features make it possible for any student to master the material — by supporting their individual learning. After all, students in such introductory courses have quite diverse backgrounds and strikingly different perspectives on the courses’ formal aspects. Students from the arts or from the humanities may need more examples and, very importantly, more time to absorb material and to practice with helpful feedback; it is remarkable how well they actually can do.

The presentation is multi-modal: each chapter is introduced by a concise lecture that formulates its central notions and techniques and motivates its learning objectives. In the main text, each central concept is also introduced by a brief lecture; each important technique is examined and used in a particular example. That kind of discussion is followed by interactive learning environments, namely, “Did I get this?” exercises that are essentially multiple-choice problems, and “Learn by doing” exercises that are genuine cognitive tutors. The most sophisticated ILE is the LogicLab.

The course material is carefully scaffolded and has been iteratively improved — using the feedback of both the many students who have taken the course and their instructors. Each chapter features review materials and assignments that include both quizzes and lab problems. The quizzes and practice questions provide fully automated feedback to students. The practice derivation problems offer support by the Dynamic Tutor. In sum, the course and all its ILEs support the individual learning of students.

For Individual Learners (who want to obtain a certificate) and students at academic institutions, the active engagement is strengthened even further: They can access the Standalone LogicLab to formulate and explore their own logical problems.
The LogicLab
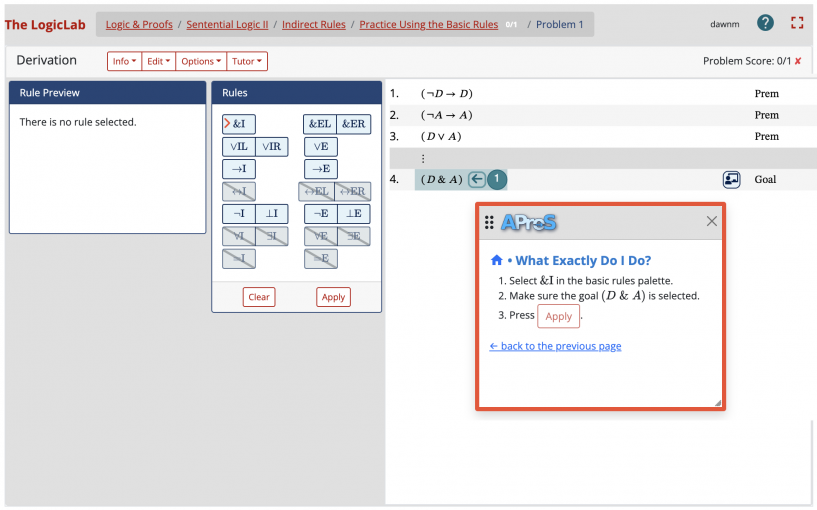
The central logical skills are developed in the LogicLab lab environment mentioned earlier. In derivation problems, students practice proof construction in a natural deduction framework.
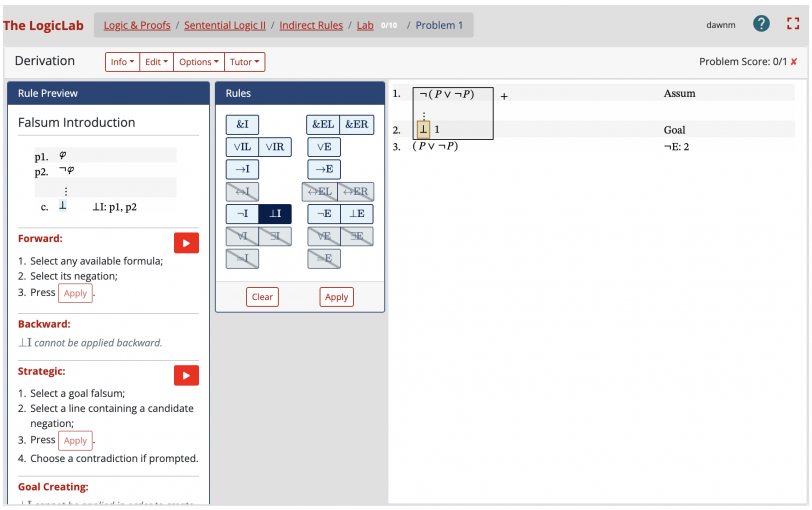
Here, their learning is supported by an intelligent automated tutor. This Proof Tutor helps students, on demand and dynamically, to think through arguments in a systematic and strategic fashion. The Proof Tutor uses the automated proof search mechanism AProS to provide, as part of the dialogue with the student, strategically informed hints for solving proof problems.
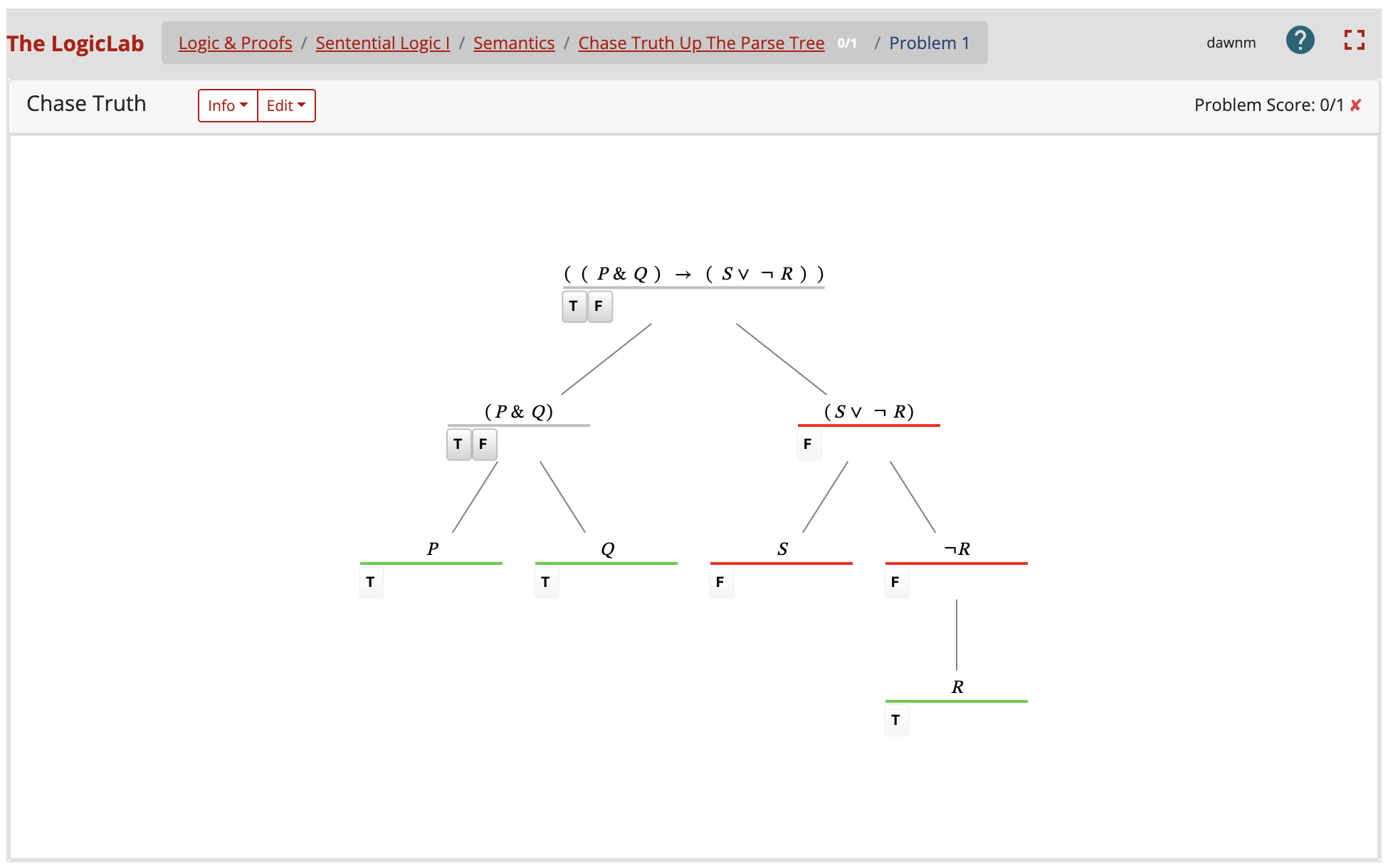
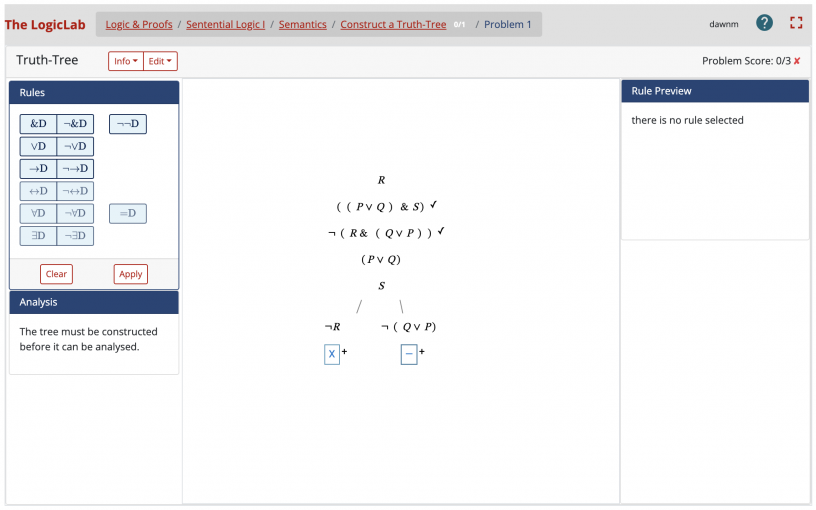
In the semantic truth-table and truth-tree problems, students practice techniques for a semantic analysis of formulae and arguments. They begin with “chasing truth up the tree of grammar”, in Quine’s vivid language; then they complete truth-tables and build truth-trees for sentential and predicate formulae involving identity. Ultimately, they learn how to define counterexamples to incorrect arguments using a completed truth-tree.
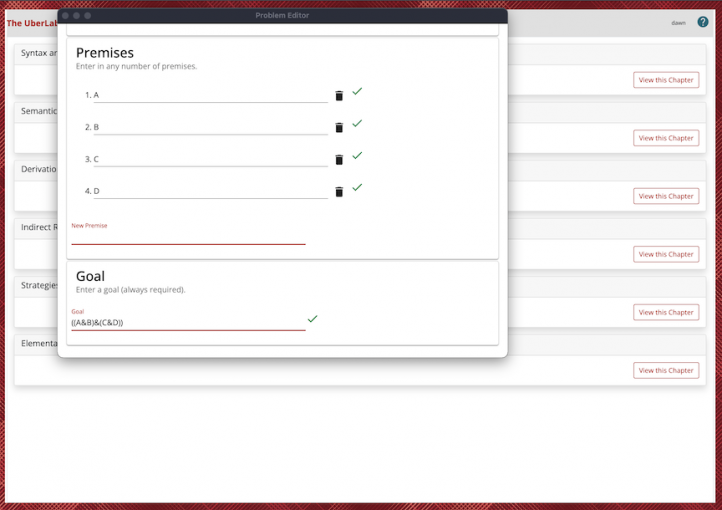
Of course, there is also the task of first checking whether a particular string of symbols is a formula of the language of sentential or predicate logic; that is done in an appropriate interface. In the course itself, all these tasks are “fixed” in the OLI framework. That is why a Standalone LogicLab has been built; it is fully independent of the OLI platform. In the Standalone LogicLab, Independent Learners and students, but also instructors, at academic institutions can formulate and explore their own logical problems. However, for obvious reasons, the dynamic support of the Proof Tutor is not provided in the Standalone.
Individual Learner
Logic & Proofs is available for individual learners in two different modes. The first mode is the completely free version. This version does not include the chapter assignments or any exams; it is to be used for a detailed, free exploration of modern logic and this novel approach to logic instruction. In particular, the chapters’ practice problems for the construction of proofs allow appeals to the supportive Dynamic Proof Tutor.
Then there is, secondly, the certificate version that carries a small registration fee of $80. Here the individual student has access to the full course content of Logic & Proofs (but without Instructor or TA support, and not including any exams). As in the free version, the chapters’ practice problems allow, when involving the construction of proofs, appeals to the Proof Tutor. The assignments do not; they give students the opportunity to demonstrate the mastery of their logical skills. All the chapter assignments are graded automatically and provide informative feedback.

A Carnegie Mellon Certificate is obtained by solving more than 75% of the Quizzes and Lab problems; if learners solve more than 90%, they obtain a Certificate with distinction.
Finally, in the certificate version, the learner has also access to the standalone version of the LogicLab, i.e., a free-standing application that has all the features of the online version. The standalone LogicLab goes beyond the course labs in that it allows students to formulate their own problems and then to solve them in the same fashion as the problems contained in the course material.
Academic Use
At Carnegie Mellon and elsewhere, Logic & Proofs is offered as a semester-long or quarter-long course with varying degrees of instructor and TA support.
- At CMU, in addition to working through the online material at a specified rate (approximately one chapter per week), the class meets in small groups once a week for an instructor-led discussion session. Active student participation is not only encouraged, but required.
- At some institutions, Logic & Proofs is used as the main resource for a course with traditional weekly lectures, as well as meetings with a TA.
- At yet other institutions, Logic & Proofs has been offered as a fully self-paced course, with online and drop-in instructor and/or TA support, but without regular class meetings.
In all three modes of use, Logic & Proofs has been found pedagogically effective. See the relevant research by Patchan, Schunn, Sieg, and McLaughlin at the AProS project site.
As of the beginning of 2023, the course has been taken for credit by nearly 14,000 students at various institutions including Carnegie Mellon University, Carnegie Mellon Qatar, IUPUI, Francisco Marroquín University (Guatemala), Habib University (Pakistan), Haverford College, University of British Columbia, University of Nevada in Las Vegas, Kent State University, College of Lake County, University of Washington, University of Maryland (College Park), and the University of South Florida.
Instructor Options and Choices
For instructors wishing to try out or start using Logic & Proofs, there are several versions of the material available in the OLI Course Builder, accessible via an instructor’s account on OLI:
- The full course, designed for the semester system (13+ weeks), including identity as a core chapter and with functions available as an additional topic. This version includes three midterms and one final exam.
- The full course, designed for the semester system (13+ weeks), including predicate logic only in the core topics, with both identity and functions available as additional topics. This version includes three midterms and one final exam
- A slightly reduced course, designed for the quarter system (10 weeks), including identity as a core chapter and with functions available as an additional topic. This version includes one midterm and one final exam.
- Sentential logic only. This version includes a final exam.
The exams included in these versions are optional. They can be removed from the course syllabus in the Course Builder, or left in but not assigned, instead serving as optional practice activities. We also have available versions of the material that include different numbers of exams, with the exam timing being somewhat different. Please contact us for details if you are interested in the possibility of using a different exam suite.
For instructors wishing to include functions as a core topic, or make any other alterations to the selection of core vs additional material, we are able to accommodate most such requests (given advance notice), and are happy to work with you to determine the best selection of core material to suit your needs.
The versions of the material mentioned above make all lab problems available to students at all times. We also offer precondition versions with the same content and exam options as those above that restrict access to lab problems as follows: students must complete in-chapter lab activities to unlock the chapter review problems, and must complete the review problem sets (by finishing at least one problem in each set) in order to unlock the chapter lab assignment. Instructors interested in using these additional preconditions in their sections should please contact us for more information and assistance setting up a course that uses them.
Detailed Content
| Introduction | |
|---|---|
| Statements and Arguments | |
| The central logical notions of statements and arguments are introduced. The notion of the standard form of an argument is presented, as are the criteria adopted for judging the quality of an argument. | |
| Learning objectives: |
|
| Sentential Logic | |
| Syntax and Symbolization | |
| The syntax of the language of sentential logic is introduced. Translation to and from sentential formulae and syntactic analysis of expressions is the focus. | |
| Learning objectives: |
|
| Semantics | |
| The semantics of the language of sentential logic are discussed. The notions of truth-values and truth-functions are introduced, and a number of semantics tools for the evaluation of both formulae and arguments are presented. | |
| Learning objectives: |
|
| Derivations | |
| The notion of a derivation is introduced, and the inference rules for the binary connectives are presented. | |
| Learning objectives: |
|
| Indirect Rules | |
| The inference rules relating to negation are introduced. | |
| Learning objectives: |
|
| Strategies and Derived Rules | |
| Strategies for completing derivations efficiently and easily are discussed, and a number of derived rules of inference are presented. | |
| Learning objectives: |
|
| Elementary Metamathematics | |
| A number of metamathematical notions are introduced and a new connective is added to the language. | |
| Learning objectives: |
|
| Predicate Logic | |
| Syntax and Semantics I | |
| The first step in the transition from sentential to predicate logic is taken, by introducing the notions of predicates and singular terms. | |
| Learning objectives: |
|
| Syntax and Semantics II | |
| The transition from sentential to predicate logic is completed by introducing the notions of quantifiers and variables. | |
| Learning objectives: |
|
| Derivations | |
| The derivation system for sentential logic is expanded to cover predicate arguments, by adding introduction and elimination rules for the quantifiers. | |
| Learning objectives: |
|
| Strategies and Derived Rules | |
| The strategies for efficient derivation completion are reconsidered in the predicate context, and a number of derived rules for predicate logic are presented. A normal form for predicate logic, called prenex normal form, is also introduced. | |
| Learning objectives: |
|
| Identity | |
| The notion of identity is introduced and discussed, and additions are made to the syntax, semantics, and derivation system in order to incorporate this notion. | |
| Learning objectives: |
|
| Functions | |
| The notion of functions is introduced and discussed, and additions are made to the syntax and semantics in order to incorporate this notion. | |
| Learning objectives: |
|
Versions and Features
| Features | Individual Use | Academic Use | |||
|---|---|---|---|---|---|
| Independent | Certificate | Sentential | Full Course | ||
| Logic Only | Quarter | Semester | |||
| free | $80 | $40/student | $80/student | ||
| Content | |||||
| Introduction | ✓ | ✓ | |||
| Sentential Logic | ✓ | ✓ | |||
| Predicate Logic | ✓ | — | ✓ | ||
| End-of-Chapter Practice | |||||
| Quiz Questions | ✓ | ||||
| Lab Exercises | ✓ | ||||
| End-of-Chapter Assignments | |||||
| Chapter Quiz | — | ✓ | |||
| Lab Assignment | — | ✓ | |||
| LogicLab | |||||
| Proof Tutor | available on selected practice problems | ||||
| Standalone Version | — | ✓ | |||
| Exams | |||||
| Midterm Exams | — | ✓ 1 | ✓ 1 | ✓ 3 | |
| Final Exam | — | ✓ | |||
More about the Independent Version…
| Open & Free Courses |
Freeforever |
| Open & Free OLI courses enable independent learners to study a subject on their own terms, at their leisure. Courses are: |
| Self-guided. ✓ |
| Self-paced. ✓ |
| Self-supported. ✓ |
| Open & Free courses include only the learning materials: |
| No teacher. ✗ |
| No tests. ✗ |
| No college credit. ✗ |
| No certificate of completion. ✗ |
*If your teacher gave you a Course Key, do not use an Open & Free course because your teacher will never see your work.
How to Access Logic & Proofs
CMU Instructors’ note: before following any of these links, please sign out of Canvas.
- Curious Explorers: Open & Free version
- Independent Learners: Self-paced with certificate of completion available
- Instructors: academic version (create an instructor account)
Open & Free features
Open & Free Courses
- Open & Free OLI courses enable independent learners to study a subject on their own terms, at their leisure. Courses are:
- Self-guided.
- Self-paced.
- Self-supported.
- Open & Free courses include only the learning materials:
- No teacher.
- No tests.
- No college credit.
- No certificate of completion.
- *If your teacher gave you a Course Key, do not use an Open & Free course because your teacher will never see your work.